本帖最後由 hlperng 於 2019-7-17 22:00 編輯
因次 (dimension),也就是數學公式中數學符號的單位,在以數學公式建立工程模型描述事物時,單位是非常重要的考量因素,因為模型的表達方式,將影響著閱讀者或學習者對公式的理解性,以及它在應用時的範疇。
舉例來說,一般在進行常態分佈的變異數的區間推定時,大部分的教科書都如下寫著:
若使用同樣的數學符號,但是將上式改寫為如下式所示:
在上面兩個式子中,使用的數學符號有 n、S2、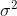 、 、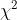 ,這些數學符號的定義,n 為樣本數、S2 為樣本變異數、 ,這些數學符號的定義,n 為樣本數、S2 為樣本變異數、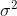 為群體變異數、 為群體變異數、) 為自由度為 (n-1) 的卡方分布的隨機變數。 為自由度為 (n-1) 的卡方分布的隨機變數。
這兩種數學表達式,從數學觀點都是一樣的,兩者都說明可以用卡方分佈隨機變數來描述 n、S2、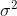 三個數之間的關係。但是,那一種表達式比較能體會其背後的意義?也就是說當應用時,那一種比較有 Fu、有感覺,而不會覺得只是套公式或帶公式而已。 三個數之間的關係。但是,那一種表達式比較能體會其背後的意義?也就是說當應用時,那一種比較有 Fu、有感覺,而不會覺得只是套公式或帶公式而已。
首先,除式是比值的概念,所以,上述兩種表達式的問題變成:誰比誰是卡方分佈?
依此,第一個數學式子的意義可以解讀為,(n-1)S2 與 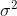 兩個數的比值為自由度 ( 兩個數的比值為自由度 (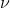 ) 為 (n-1) 的卡方分佈的隨機變數,問題在於 S2 為何要乘以 (n-1),其在實際應用時的意義為何? ) 為 (n-1) 的卡方分佈的隨機變數,問題在於 S2 為何要乘以 (n-1),其在實際應用時的意義為何?
根據機率與統計理論,S2是樣本變異數,亦即隨機變數抽樣值計算得到的二階統計量,n 為樣本數,卡方分布的自由度 (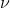 ) 為樣本數減 1,亦即 ) 為樣本數減 1,亦即 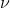 = n - 1,是抽樣過程樣本數值進行二階統計量資料分析時的自由度,而 S 2/(n-1) 則代表群體平均數的變異數。所以,第二個數學式子為群體本身的變異數與群體平均數的變異數之間的比值。 = n - 1,是抽樣過程樣本數值進行二階統計量資料分析時的自由度,而 S 2/(n-1) 則代表群體平均數的變異數。所以,第二個數學式子為群體本身的變異數與群體平均數的變異數之間的比值。
看看下圖,綠色曲線為原始隨機變數 (X) 的分布曲線,紅色為平均數 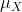 的分布曲線。是否有些新的發現!誰與誰的比值是卡方分佈? 的分布曲線。是否有些新的發現!誰與誰的比值是卡方分佈?
| 